投稿
  1. 副业富首页
  2. 杂谈

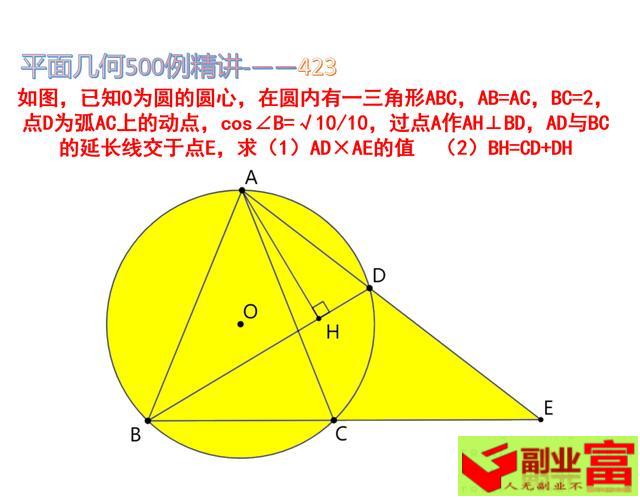
hd和bd的区别是什么（圆O，AB=AC，BC=2，cos∠B=√1010，AH⊥BD，求AD×AE，BH=CDDH）

业副 • • 杂谈 • 阅读 22
hd和bd的区别是什么（圆O，AB=AC，BC=2，cos∠B=√1010，AH⊥BD，求AD×AE，BH=CDDH）

题目：
如图，已知O为圆的圆心，在圆内有一三角形ABC，AB=AC，BC=2，点D为弧AC上的动点，cos∠B=√10/10，过点A作AH⊥BD，AD与BC的延长线交于点E，求（1）AD×AE的值 （2）BH=CD+DH

粉丝解法1：
1）adb相似abe，ad：ab=ab：ae，得10。
2）AD×BC＋AB×CD＝BDxAC（托密勒定理）
AD＝√10HD
BD＝BH＋DH
2√10DH＋√10CD＝√10〈BH＋DH〉
∴BH＝CD＋DH

粉丝解法2：
1）AB=1/cosB=√10，∠ADB=∠ACB=∠ABC，△ADB∽△ABE，AD*AE=AB2=10，
2）作AF⊥CD交其延长线于F，
则△ADH≌△ADF(AAS)，
HD=DF, AB=AC，
∠ABH=∠ACF，
△ABH≌△ACF，
BH=CF=CD+DF=CD+HD

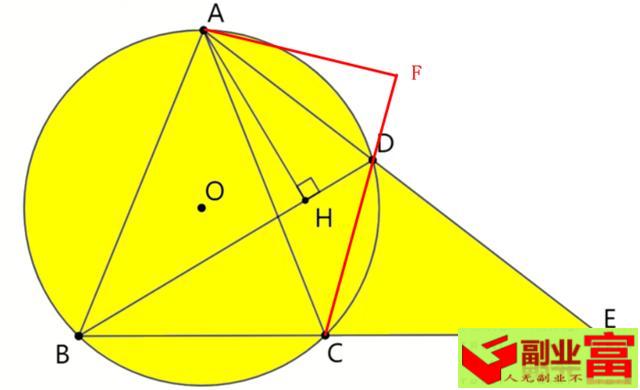
hd和bd的区别是什么（圆O，AB=AC，BC=2，cos∠B=√1010，AH⊥BD，求AD×AE，BH=CDDH）

粉丝解法3：
解：连接CD，∵AB=AC，∴∠ACB=∠ABC，
∵四边形ABCD内接于圆O，
∴∠ADC+∠ABC=180°，
又∵∠ACE+∠ACB=180°，
∴∠ADC=∠ACE，
∵∠CAE=∠CAD, ∴△EAC∽△CAD，

∴AC:AD=AE:AC

∴AD*AE=AC2=AB2=（√10）2=10.

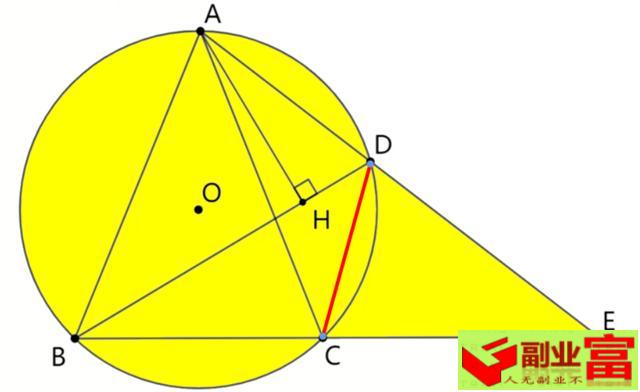
hd和bd的区别是什么（圆O，AB=AC，BC=2，cos∠B=√1010，AH⊥BD，求AD×AE，BH=CDDH）

证明：在BD上取一点N，使得BN=CD，
在△ABN和△ACD中，
AB=AC ，∠3=∠1， BN=CD

∴△ABN≌△ACD(SAS)，

∴AN=AD, ∵AH⊥BD,AN=AD, .·.NH=DH,
又∵BN=CD，NH=DH，
∴BH=BN+NH=CD+DH。

hd和bd的区别是什么（圆O，AB=AC，BC=2，cos∠B=√1010，AH⊥BD，求AD×AE，BH=CDDH）

#把地球的故事讲给宇宙#

创业项目群，学习操作 18个小项目，添加 微信：2860016296  备注：小项目！

本文内容均来自互联网或用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌抄袭侵权/违法违规的内容， 请发送邮件至(laxie2022@qq.com)举报，一经查实，本站将立刻删除。
如若转载，请注明出处：https://www.fuyefu.com/20264.html
赞 (0)
业副业副
0
上一篇 2023年3月4日 am11:54
下一篇 2023年3月4日 am11:54

相关推荐

在线投稿
公众号